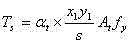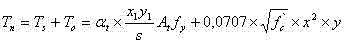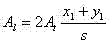Dimensionamiento de Vigas

Dimensionamiento de Vigas Sometidas a Torsión

Se presenta un análisis simplificado para dimensionar una viga sometida a torsión. La imagen a continuación muestra la superficie de falla parcialmente fisurada, que incluye la parte de compresión del hormigón (zona sombreada) y las fuerzas horizontales y verticales de los estribos S_h y S_v para todos los estribos que atraviesan la superficie de falla, excepto para aquellos localizados en la zona de compresión.

Torsión en vigas. Superficie de falla en flexión oblicua.

La cantidad de ramas de estribos horizontales en la parte superior o inferior que atraviesan la superficie puede calcularse con n_h= (X₁ cotφ)/s, siendo “s” la separación; la cantidad de ramas verticales del lado opuesto a la zona de compresión es igual a n_y = y/s. Con base en ensayos, se sabe que en la falla las ramas de los estribos verticales fluyen, mientras que las ramas horizontales no están por lo general en la tensión de fluencia. Según este supuesto, el par de torsión producido por las fuerzas de estribos horizontales es:

  (a)

     

Donde A_t es el área de una rama de estribos, f_sh es la tensión de una rama de un estribo horizontal, f_y es la tensión de fluencia del acero, S_h es la fuerza horizontal de estribo y k_h = cotφ . (f_sh/f_y).

Para analizar el momento torsor generado por las tensiones de estribos verticales cerca de la cara del frente, debe observarse primero que las tensiones de equilibrio cercanas a la cara posterior en la zona de compresión, son claramente indeterminadas. Estas constan de, por lo menos, una tensión cortante S_c y una tensión de compresión P_c en el hormigón, y tensiones en las ramas de los estribos localizados en esa zona. Sin embargo, es claro que a causa del equilibrio todas estas fuerzas deben tener una resultante R igual y opuesta a la suma de las tensiones de los estribos verticales S_v. Por lo tanto, el momento torsor producido por las tensiones de estribos verticales puede formularse:

(b)

Donde X_v es el brazo de palanca de las tensiones internas S_v y R siendo k_v = x_v/x₁.

Puede observarse que las ecuaciones (a) y (b) son idénticas, excepto para kh y kv. En esta fase de conocimientos, ninguna de estas constantes puede determinarse en forma analítica y es preciso recurrir entonces a efectuar muchos ensayos. Se define α_t = k_h + k_v, la contribución total de los estribos al momento torsor, T_s = T_v + T_h es igual a:

Diversos ensayos demuestran que α_t depende principalmente de la relación de las dimensiones de la sección transversal y puede tomarse igual a:

Anteriormente se menciono que, después de que se genera el fisuramiento, la contribución de la zona de compresión del hormigón al momento torsor, T_o, aproximadamente es igual a la mitad del momento torsor de fisuramiento, T_cr. Si se toma esta fracción en forma conservadora como el 40%, se llega a:

La resistencia a la torsión nominal total es:

A partir de la deducción de T_n resulta evidente que esta resistencia nominal a torsión se desarrollara únicamente si los estribos tienen un espaciamiento suficientemente cercano, para que cualquier superficie de falla sea atravesada por una cantidad adecuada de estribos. Por esta razón se establecen límites de espaciamiento máximo para los estribos.

El papel del refuerzo longitudinal en el suministro de resistencia torsional no es claro todavía, pero se sabe que T_n puede desarrollarse únicamente si se suministra un apropiado refuerzo longitudinal. Sus principales funciones son las siguientes:

1. Anclar los estribos, particularmente en las esquinas ya que esto les permite desarrollar su resistencia a la fluencia completa.
2. Proporcionar al menos una parte del momento torsor resistente, gracias a las fuerzas de dovela que se producen cuando las barras atraviesan grietas torsionales.
3. Se observa que, después del fisuramiento, los elementos sometidos a torsión tienden a alargarse en la medida en que las grietas en espiral se ensanchan y se hacen mas pronunciadas. El esfuerzo longitudinal contrarresta esta tendencia y controla al ancho de las fisuras.

Los ensayos realizados indican que para que la ecuación de la resistencia de la torsión nominal sea valida, el volumen total de acero longitudinal en una unidad de longitud del elemento que debe estar entre 0,70 y 1,50 veces el volumen total de estribos en esa misma longitud. Se acostumbra a diseñar los elementos a torsión de manera que estos dos volúmenes sean iguales. Esto se verifica fácilmente porque se cumple siempre y cuando el área total del esfuerzo longitudinal sea:

Torsión en vigas de Hormigón Armado

Torsión en Elementos de Hormigón Armado

Para resistir la torsión, el refuerzo debe estar conformado por estribos poco espaciados y por barras longitudinales. Diversos ensayos evidencian que las solas barras longitudinales aumentan muy poco la resistencia a la torsión, lográndose incrementos de un 15% como máximo. Esto es comprensible puesto que la única forma en que las barras longitudinales pueden contribuir a la resistencia a la torsión en vigas es mediante la acción de dovelas que, en particular, es débil y poco confiable si el fracturamiento longitudinal a lo largo de las barras no está restringido por estribos. Así que, la resistencia a la torsión de elementos armados únicamente con aceros longitudinales puede estimarse en forma satisfactoria y algo conservadora, con las ecuaciones siguientes:

   (1)

  

  (2)

Cuando los elementos se arman en forma adecuada, como se muestra a continuación, las fisuras en el hormigón aparecen para un momento torsor igual o un poco mayor que el de un elemento de hormigón simple (ecuación 2). Las fisuras forman un patrón en espiral, como aparece a en la figura (1-b), para una sola fisura.

Fisura de torsión en vigas de hormigon armado (1).

En realidad se desarrollan una gran cantidad de fisuras similares en forma de espiral con muy poco espaciamiento entre si. Después de la fisuración, la resistencia a la torsión del hormigón disminuye hasta casi la mitad de la resistencia del elemento no fisurado y el resto de la torsión ahora la resiste la armadura. Esta distribución en la resistencia interna se refleja claramente en la curva de momento torsor versus ángulo de torsión (figura siguiente), que al nivel del momento torsor de fisuración genera rotación continua para momento torsor constante, hasta que la armadura toma la porción del momento torsor que el hormigón ya no es capas de resistir.

Curva momento torsor-ángulo de torsión en vigas de hormigón armado

La armadura debe resistir, entonces, cualquier incremento adicional del momento torsor aplicado. La falla ocurre cuando en alguna zona a lo largo del elemento se presenta el aplastamiento del hormigón en una línea como la a-d de la figura (1). En un elemento bien diseñado, este aplastamiento ocurre después que los estribos comienzan a fluir.

La resistencia a la torsión puede analizarse teniendo en cuenta el equilibrio de las fuerzas internas que se transmiten a través de la superficie de falla potencial como aparece en la parte sombreada de la figura (1-b). Se observa que está limitada por una grieta de tracción a 45º a través de la cara más ancha, dos grietas en la cara mas delgada con una inclinación φ, ángulo que generalmente está entre 45º y 90o, y la zona de aplastamiento del hormigón a lo largo de la línea c-d. Al igual que para las vigas de hormigón simple, la falla se presenta básicamente por flexión con una zona de compresión en el concreto que se produce al lado de la línea b-c.

Fuente: Facultad de ciencias exactas, físicas y naturales

               Universidad nacional de Córdoba

Torsión en Vigas

Torsión en Vigas de Hormigón Simple - Continuación

Las tensiones cortantes actúan en pares sobre un elemento cerca de la superficie ancha, como aparece en la siguiente figura. Como se demuestra en cualquier texto de resistencia de los materiales, este estado de esfuerzos es equivalente a un estado de esfuerzos de tracción y compresión iguales en las caras de un elemento rotado a un ángulo de 45^o con respecto a la dirección del cortante. Estos esfuerzos de tracción inclinados son del mismo tipo que los causados por cortantes transversales. Sin embargo, para el caso de la torsión, puesto que las fuerzas cortantes por torsión en vigas tienen signos opuestos en las dos mitades del elemento (figura b), los esfuerzos de tracción diagonal correspondientes en las dos mitades forman ángulos rectos entre si (Figura a).

Descomposición de esfuerzos por torsión en vigas

Cuando los esfuerzos de tracción diagonal exceden la resistencia a la tracción del hormigón, se forma una fisura en forma accidental en algún sitio más débil y ésta se propaga inmediatamente a través de la viga (debido a la torsión en vigas), como se ilustra en la figura anterior. Puede observarse que las figuras de tracción (en la cara más cercana de la figura (a)) se forma prácticamente a 45^o, es decir, en dirección perpendicular a la de los esfuerzos de tracción diagonal. Las fisuras en las dos caras menores, donde los esfuerzos de tracción diagonal son menores, tienen una inclinación menos definida como se señala, y la línea de fractura en la cara más lejana une las fisuras en las caras menores. Esto completa la formación de una superficie de fractura completa a través de la viga, que produce la falla del elemento por la torsión en vigas.

Para propósitos de análisis, esta superficie de fractura un poco alabeada puede reemplazarse por una sección plana inclinada a 45^o con respecto al eje, como se presenta en la figura (b). Las observaciones de ensayos realizados demuestran que para este plano, la falla se produce más por flexión que por torsión en vigas misma. Como en las figuras (b) y (c), el momento torsor aplicado T puede descomponerse en un componente T_b que causa flexión con respecto al eje a-a del plano de falla y otro componente T_t que ocasiona la torsión de la sección inclinada.

Puede verse que:

                             T_b = T cos 45^o

El modulo de flexión alrededor del eje a-a es:

El esfuerzo máximo de tracción por flexión en el hormigón es:

Puede observarse que esta tensión de tracción es idéntico al esfuerzo de St. Venant, τ_max, o la tensión diagonal correspondiente, σ, para α =1/3.

Si f_tb fuera el único esfuerzo en acción, la fisuración ocurriría cuando f_tb = f_t, la tensión de rotura del hormigón que puede tomarse es igual a f_t = (0,623√f`<sub>c</sub>) con f`_c en MPa, para hormigones de densidad normal. Sin embargo existe un esfuerzo de compresión f_cb de igual magnitud que forma un ángulo recto con el esfuerzo de tracción f_tb. Para este estado de esfuerzos biaxiales, los ensayos demuestran que la presencia de una compresión perpendicular igual, reduce la resistencia a la tracción del hormigón en casi un 85%. En consecuencia, se formara la grieta y se presentara la falla del elemento debido a la torsión en vigas aproximadamente cuando f_tb = 0,85 f_t = 0,53 √f`_c. Puede, entonces, tomarse este valor de f_tb como el esfuerzo de agrietamiento:

           

Se sustituye el valor de f_tb en la ecuación anterior por el de f_cr y se obtiene la magnitud del momento torsor que producirá el agrietamiento y la falla en un elemento rectangular de hormigón simple (torsión en vigas):

 

 

Torsión en Vigas

Torsión en vigas de hormigón simple

La figura siguiente (a) señala una porción de elemento prismático sometido a momentos torsores T iguales y opuestos en sus extremos. Si el material es elástico, la teoría de torsión de St. Venant indica que los esfuerzos cortantes por torsión en vigas se distribuyen sobre la sección transversal como en la figura (b). Los mayores esfuerzos cortantes se presentan en la mitad del lado mayor de la sección y son equivalentes a:

Donde α es un factor de forma aproximadamente igual a 0,25, y X e Y respectivamente, son los lados cortos y largos del rectángulo. Si el material es inelástico, la distribución de esfuerzos es similar y se señala con líneas punteadas en la figura (b), y el valor máximo del esfuerzo cortante todavía lo da la ecuación anterior, excepto que α tiene un valor mayor.

Figura (a): Tensión causada por torsión en vigas. Figura (b) tensión en la sección.

La figura siguiente muestra las tensiones maximas para diferentes secciones de elementos utilizados en la construcción.

La torsión en vigas o elementos es resistida de una mejor manera por secciones circulares o anulares, puesto que hay una mejor transferencia del esfuerzo entre una sección y otra.

Torsión en Vigas

Torsión en Vigas - Comentarios

Los elementos de hormigón armado están sometidos comúnmente a momentos flectores, a fuerzas cortantes asociadas con momentos flectores y en el caso de columnas, a fuerzas axiales combinadas a menudo con flexión y cortante. Además, pueden actuar fuerzas torsionales que tienden a tienden a retorcer el elemento con respecto a su eje longitudinal. Las fuerzas torsionales rara vez actúan solas y casi siempre están acompañadas por momentos flectores, por cortantes y algunas veces por fuerzas axiales. Generalmente se da la torsión en vigas cargadas excéntricamente.

En tiempos anteriores, la torsión en vigas se observaba como un efecto secundario y no era tenida en cuenta en forma explicita en el diseño; su influencia era absorbida por el factor de seguridad global (el autor prefiere llamarlo “factor de ignorancia”, ya que esta para cubrir esos factores que no podemos determinarlos con certidumbre) de estructuras conservadoramente. Sin embargo, en estos años surgió la necesidad de considerar en muchos casos los efectos torsionales en el diseño de elementos y proporcionar refuerzos para aumentar la resistencia torsional.

Existen dos razones principales para este cambio. La primera se relaciona con el mejoramiento en los métodos de análisis y diseño, como el método de diseño a la rotura que ahora se utiliza, los cuales permiten un factor de seguridad global un poco menor mediante una evaluación mas precisa de la capacidad de carga y conduce a su vez a elementos con dimensiones un poco menores. La segunda razón tiene que ver con el incremento en el uso de de elementos estructurales en los cuales la torsión es un aspecto principal de su comportamiento, como la torsión en vigas de puentes curvos, la torsión en vigas cajón cargadas excéntricamente y la torsión en losas de escaleras helicoidales.

Al considerar efectos de torsión en vigas estructurales de hormigón armado, es importante diferenciar entre torsión primaria y torsión secundaria. La torsión primaria, algunas veces llamada torsión de equilibrio o torsión estáticamente determinada, se presenta cuando la carga externa no tiene otra alternativa que ser resistida por torsión. La torsión secundaria, también llamada torsión por compatibilidad o torsión estáticamente indeterminada, sino se arma a torsión la viga no hay peligro de colapso.

Imagen de torsion en vigas

Se deberá igualmente disponer de una armadura de momento flector negativo en la unión losa-viga para evitar la fisuración.